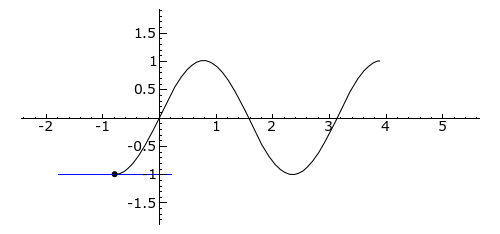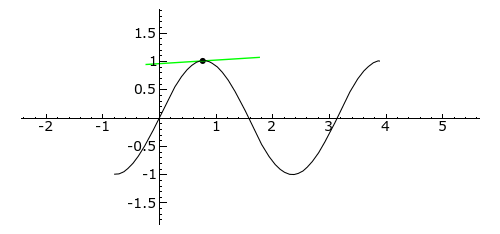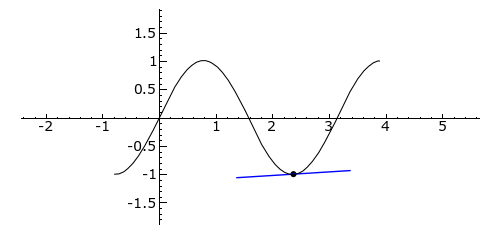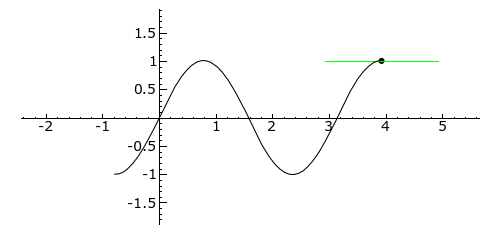
Inflection points in differential geometry are the points of the curve where the curvature changes its sign. In the illustration below, it is when the tangent turns red or when the curve intersects with the X axis in this case.
The 2nd illustration shows how a rotation of circle can be represented as a sine curve. In this case, the tracing of a dot on the circle starts at 3 o’clock and goes counterclockwise. The inflection point is at 9 o’clock, at which the dot starts the 2nd half of the circle, and is on its way back to the starting point.
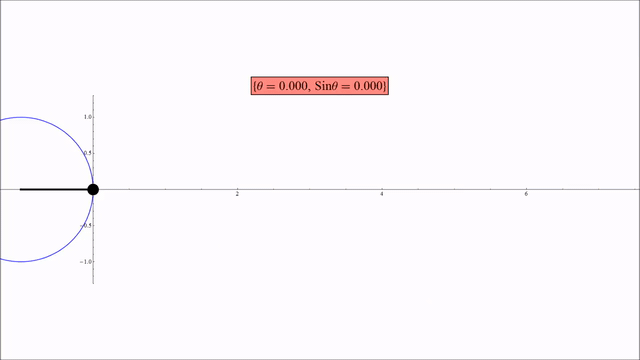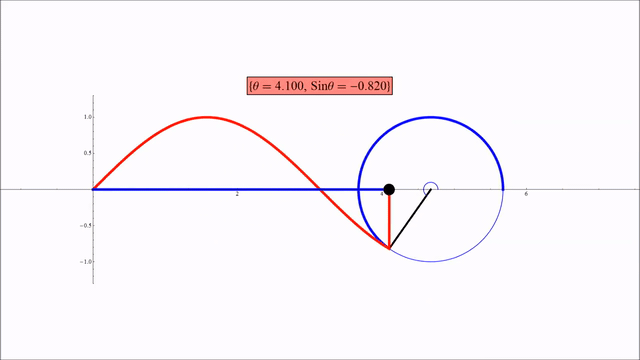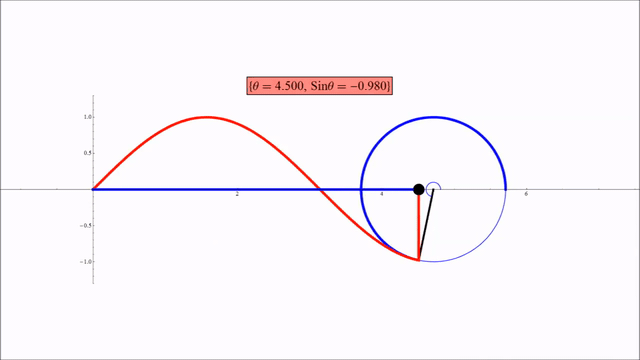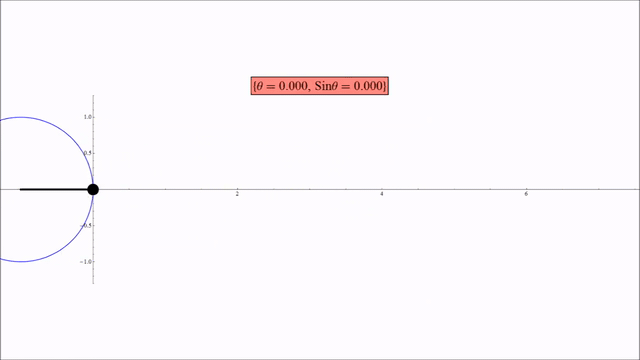
Simply put, it is the midpoint of an S-curve, which actually represents a taiji circle as described in http://practicalmethod.com/2016/12/s-curve-is-really-the-circle/.
Master Chen Zhonghua always emphasizes the need to go over or to the other side. What are we going over? It is the inflection point that we need to go over. The other side lies beyond the inflection point.



{ 2 comments… read them below or add one }
Great article! Related terms include the demarcation dot, threshold, point of reference.
The first illustration clearly distinguishes which side the tangent is on and when it goes to the other side.
The second illustration shows the covering of Space and Time. http://practicalmethod.com/2012/06/space-and-time-online-video-trailer/